=================================
/ p.3 /
BRIEF OBSERVATIONS,
&c.
__________
THE manuscript Arundel, 343, sometimes called the Mentz Manuscript, is a small quarto of the twelfth century, on vellum; and the first tract, entitled De Arte Numerandi, consists of four leaves only, unfortunately being imperfect at the end. A fragment from the recto of the first folio is lithographed in the appendix to the Rara Mathematica, which serves to show the style of the manuscript and the forms and names of the contractions. The treatise itself commences with an explanation of the increasing value of igin, andras, &c., in the different abacal compartments; in point of fact, a definition of abacal numeration dependent upon the principle of local decimal value. It is important to notice that, after this explanation, the compiler gives the usual definitions of digiti and articuli, clearly showing by that his comprehension of their future value. It is remarkable that everything stated is subservient to multiplication and division, no notice whatever being taken of addition, subtraction, duplation, or mediation; -- a plain proof, if any were needed, that when the boundaries were abolished, and when an attempt at a gene- / p.4 / ralization of the local system was made, artificial methods were adopted to come to the same conclusions.
And now for the modus operandi: and in order to render it intelligible to every reader, let us take the first example in multiplication, on account of its great simplicity:
"Sint ergo iiij. pedes equi, unusquisque habens vj. clavos"
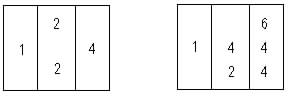
Arbas is to be placed in the lower part of the singular arc (arcus singularis), and in the upper part of the same arc is placed chalcus "quasi fundamentum multiplicationis." But in the actual multiplication recourse is had to the common Roman notation, and the result of the multiplication of arbas and chalcus in the singular arc is xxiiij. Then the system of articuli comes into operation, and the articulus of this number (24) is andras, which, by the principle of local position and of no other, is placed in the decenal arc. How can we possibly suppose a rule of this nature with its full explanation to exist, without allowing its author to have possessed the knowledge of the value of local position? The decenal arc is made use of in a simple but masterly manner, and the articulate system is invented to avoid the principal difficulty. The digit arbas, it is almost unnecessary to observe, is placed in the singular arc, and thus we have the complete number represented. In higher numbers the centenal, millenal, and other arcs come into use. The following rule is a fair specimen of the methods employed:
"Cum autem per decenum multiplicabis singularem, dices hanc regulam deceni; -- Decenus quemcunque arcum multi- / p.5 / plicat, in secundo ab eo pone digitum in ulteriori articulum," fol. 2, r o, the reason of which is obvious. Thus, in the MS., the operation for finding the square of twelve is a follows:

proceeding in a most complicated manner, but merely using the simple formula
m.(np)=mnp, or, 12 x 12 = 12 x 2 x 6 = 24 x 6,
in which latter case the above rule is applicable. This rule is afterwards generalized -- "His patefactis, oculus mentis aperiatur ad subtilitatem divisionis;" but as the same system is carried out, precisely similar to the methods of Johannes de Sacro-Bosco, it is not necessary to repeat them.
Gerbert uses the Boetian fractional notation, and I consider this fact a grant argument for his acquaintance with the Boetian contractions, if, indeed, the passage in the geometry of Boetius was not introduced by him. It does not appear to me that much authority ought to be given to the well-known passage of William of Malmesbury, as far as it is supposed to prove that Gerbert brought the knowledge of the abacus from Spain; and, as Professor Peacock so well observes, "the passage of this historian contains no certain intimation of the knowledge of the notation by nine figures / p.6 / and zero, as the rules which would be thence derived would tend rather to relieve than increase the labours of the sweating calculators," -- quae a sudantibus abacistis vix intelliguntur. Again, what difference is there between the system of the Greeks, the system in the Mentz Manuscript, the system in the passage in Boetius as satisfactorily explained by M. Chasles, and the Arabic method? I mean with regard to first principles. (M. Chasles, 'Aperc[+ cidilla]u Historique,' p.474.) All, in fact, are contained in the following formula, which is the general expression for any finite number:
![]()
where ao, a1, a2, ... am are digits, or integers less than the radix 10.
From the Mentz MS. in the Arundel Collection it is very evident that their mode of operation with the abacus had received one great improvement on the Greek and Roman system, the abolishing the necessity of motion, and only using the table cum pulvere, as a means for distinguishing position. Thus, in the following addition sum, using the names instead of the cabalistic characters, we have an example of their method of proceeding:
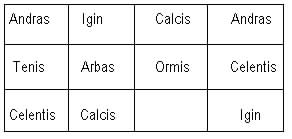
/ p.7 /
Thus making a total of -- celentis, calcis, zero, igin. Now, it is evident that, in order to do away with the necessity of this table, supposing the contractive marks again substituted for the latter words, we have only to imagine an arbitrary character for the deficiency under the ormis, and the modus operandi is synonymous with our own present form.
The following are new instances of the appearance of the zero without its use:-- MS. Hatton. 7, we find the following passage: "inscribitur et in ultimo figura 0, sipos nomine. Quae licet numerum nullum significet: tum ad alia quaedam utilis est." MS. Lansd. 842, is a contractive mark for a sipos, outside the drawing of the abacus. MS. Hatton. 112: the sipos is given with its contraction, but is only used to fill up the space in the abacus.
A passage at the end of the second book of 'Boetii Geometria', de minutiis, proves that the fractional notation was contemporary with that writer. Bede, in his Treatise on Arithmetic, has given a whole chapter to it. Next comes the Arundel MS. of the twelfth century, from which I am enabled to give a most exceedingly curious specimen of their modus operandi:
SOLUTION. Semis=as. semiuncia, but as=igin; therefore, semis=igin . semiuncia=semiuncia; because igin is the Boetian unity.
/ p.8 /
We have thus the required quantity in a very complicated form. To effect the reduction of this is the work of another long operation, which it is unnecessary to repeat here, as the above will sufficiently serve for an example of the laborious, though ingenious, plan which was pursued.
________________
PRINTED BY J.E. ADLARD, BARTHOLOMEW CLOSE


